뜌릅
기수정렬, 계수정렬 본문
기수정렬
기수정렬( radix sort )은 낮은 자리수부터 정렬해가는 것을 기본 개념으로 하는 정렬 알고리즘입니다. 기수 정렬은 비교연산을하지 않으며 정렬 속도가 빠르지만 데이터 전체 크기에 기수 테이블의 크기만한 메모리가 더 필요합니다. 일반적으로 자릿수가 고정되어 있습니다.
다음은 자연수에 대해 기수 정렬하는 과정입니다.
- 0~9까지 버킷(Queue)을 준비합니다.
- 모든 데이터에 대해 가장 낮은 자릿수부터 버킷에 알맞게 데이터를 둡니다.
- 0부터 차례대로 버킷에서 데이터를 다시 가져옵니다.
- 가장 높은 자릿수를 기준으로 하여 자리수를 높여가며 2번 3번 과정을 반복합니다.
예시
아래의 8개 데이터에 대하여 기수 정렬을 시도해 보겠습니다. 위의 그림과 같이 각 숫자에 해당하는 Queue공간을 할당하고 진행합니다.

먼저 1의 자리 숫자부터 시도를 합니다. 데이터 순서대로 각 1의 자리에 해당되는 Queue에 데이터가 들어가게 됩니다. 15같은 경우는 1의 자리가 5이므로 Queue 5에 들어가는 방식입니다.

Queue에서 빼와서 차례대로 다시 배열에 넣어주면 됩니다.

위의 그림처럼 다시 0번 Queue부터 차례대로 데이터를 가지고 와서 원래의 배열에 넣어주게 됩니다.
1의 자리에 대한 정렬이 완료되었습니다. 다음으로는 10의 자리에 대하여 같은 작업을 반복합니다.

마찬가지로 각 데이터의 10의 자리에 해당되는 Queue에 데이터를 위치 시킵니다. 그런 다음 0번 Queue부터 차례대로 다시 데이터를 가지고 옵니다.

최종적으로 정렬이 완료가 됩니다. 일반적으로 비트마스킹 연산 or 운영체제의 가상메모리에서 물리메모리의 맵핑에서 사용이 됩니다.
시간복잡도는 O(dN)입니다. d는 자릿수입니다.
안전성이 있는 정렬입니다.
계수정렬
계수정렬은 비교연산을 사용하지 않는 정렬입니다. 저희가 사용하던 quick sort, merge sort, insertion sort등은 모두 비교연산을 사용하였고 시간복잡도가 O(NlogN)이거나 O(N^2)였습니다.
비교연산을 사용하지 않는다면 Descision Tree의 비교연산을 사용하지 않게 될 것이므로 큰 장점을 갖게 될것이고 계수 정렬은 O(N + K)의 겉보기에는 압도적인 시간복잡도를 갖게 되었다. 비교연산없이 정렬을 하는 방법과 이렇게 압도적인 시간복잡도를 가졌음에도 왜 덜 덜리 사용되는지 알아보자!
기본적인 제약사항은 다음과 같다. (이게 덜 사용되는 이유..)
- 데이터(값)은 양수여야 한다.
- 값의 범위가 너무 크지 않아야 한다.(메모리 사이즈를 넘어서는 안된다. K을 의미한다.)
계수 정렬은 이름 그대로 배열 내에 특정한 값이 몇번 등장했는지에 따라 정렬을 수행하기 때문에 비교연산이 사용되지 않는다.
1과 2 제약사항이 존재하는 가장 큰 이유는, 우리가 배열의 인덱스를 이용하여 데이터를 저장할 것이기 때문이다. 따라서, 배열의 인덱스는 양수만 존재하고, 값이 너무 커지면 메모리 영역을 너무 많이 할당해버려 문제가 생기므로 위의 두 조건이 붙게되는 것이다.
계수 정렬의 아이디어는 매우 단순합니다.
[3,1,2,3,4,1,5,3]라는 배열이 존재할때, 각 배열의 요소값들을 세어서 저장합니다.
1: 2개
2: 1개
3: 3개
4: 1개
5: 1개
이 세어진 값들을 그냥 갯수대로 나열해보면 [1,1,2,3,3,3,4,5]로 정렬이 됩니다.
하지만 여기서 끝나지는 않습니다. 누적합이라는 개념을 더해야 합니다. 즉 해당 수를 갖고있는 개수뿐만 아니라 앞에 몇개의 원소가 들어와야 하는지 또한 값을 저장해야합니다.
즉 위의 배열로 설명을 하자면 누적합 배열은 [2,3,6,7,8]이 되어야 합니다. (현재 숫자 개수 + 앞에 나온 숫자 개수)
예시
A는 정렬해야 할 배열, B는 값들의 등장횟수, C는 정렬을 할 값들을 저장할 배열입니다.
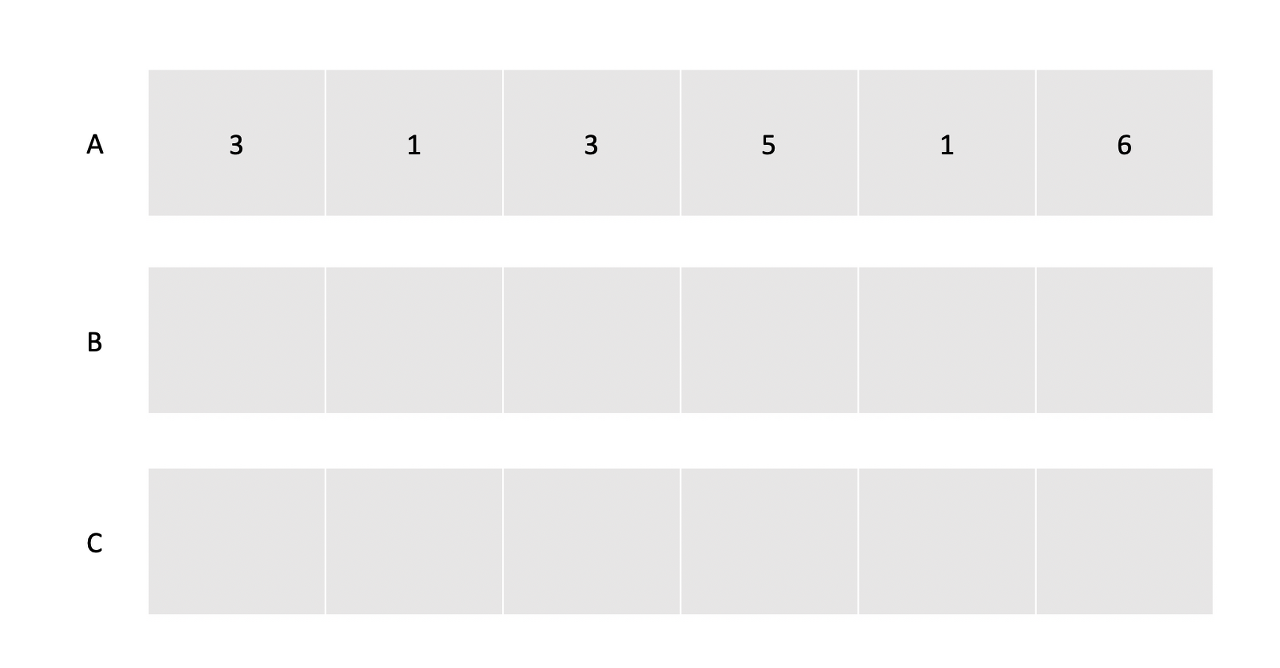
Phase1
제일 먼저 A를 순회하면서 값들의 등장횟수를 B에 저장합니다.(n번)

Phase2
한 사이클을 돌면서 B를 다시 누적합 배열로 만듭니다. (k번)

Phase3
이제 배열의 A를 뒤에서부터 순회하면서 해당 값에 해당하는 위치의 B의 값을 -1해가면서 C에 정렬합니다.(뒤에서부터 순회하는 이유는 안정된 정렬을 만들기 위해서입니다. 계산횟수는 n번)

결과
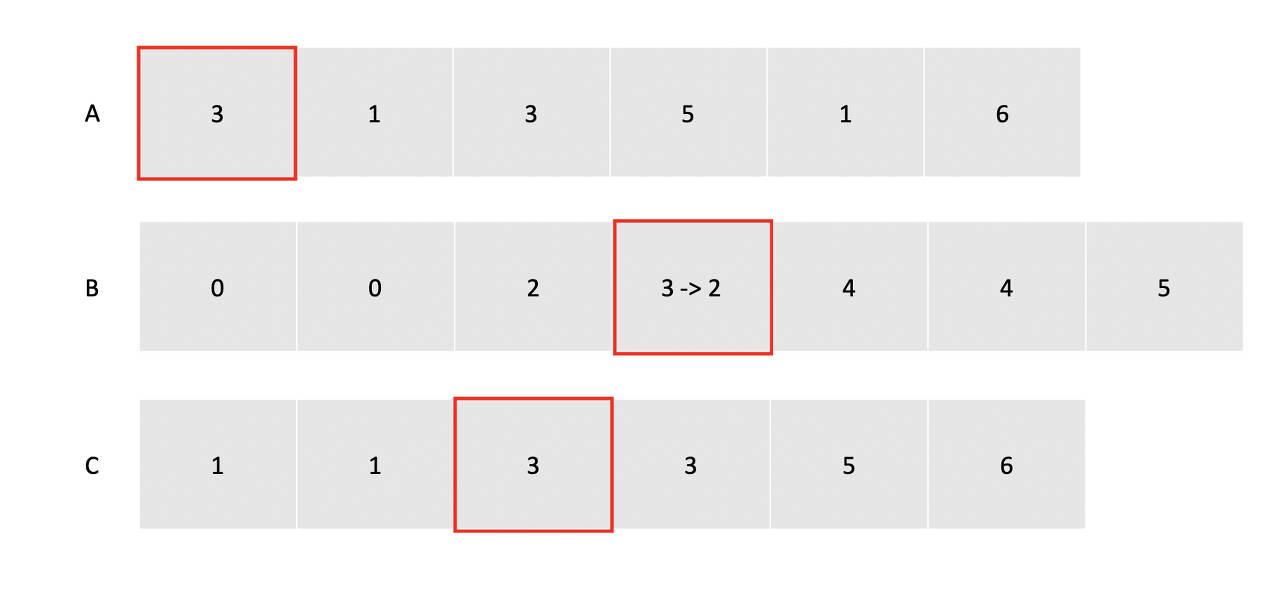
시간복잡도를 계산하자면 n+ k + n으로 O(N+K)가 됩니다.
해당 알고리즘은 아시다시피 메모리가 크게 낭비되는 경향이 있습니다. 예시와 달리 n의 크기가 1000이고 k 즉 값의 범위가 4096이라고 한다면 최소 3096개의 메모리를 낭비하게 될수 있기 때문입니다.
또한 입력받은 배열의 최댓값 즉 k의 값이 커저야 한다면 이 알고리즘은 비효율적이 됩니다. 즉 n의 크기가 크고 k의 크기가 작은 배열에 한해서 정렬이 효율적으로 동작하게 됩니다.


